Referenciais inerciais
O que são referenciais inerciais?
FÍSICA MODERNA


Isaac Newton consolidou e aprimorou as ideias de Galileu, estabelecendo as leis fundamentais do movimento que ainda são ensinadas nas salas de aula hoje. Com sua obra-prima, "Princípios Matemáticos da Filosofia Natural", publicada em 1687, Newton descreveu as três leis do movimento, conhecidas como as leis de Newton. Essas leis forneceram uma estrutura matemática precisa para entender e prever o comportamento dos corpos em movimento.


Para compreendermos as ideias de Newton sobre a relatividade de movimento, vamos imaginar a seguinte situação.
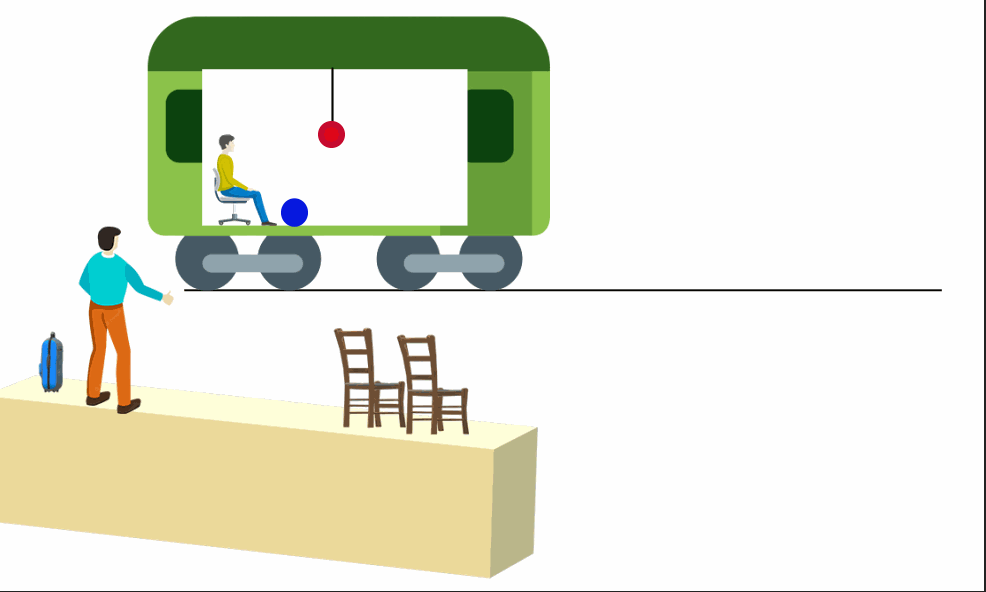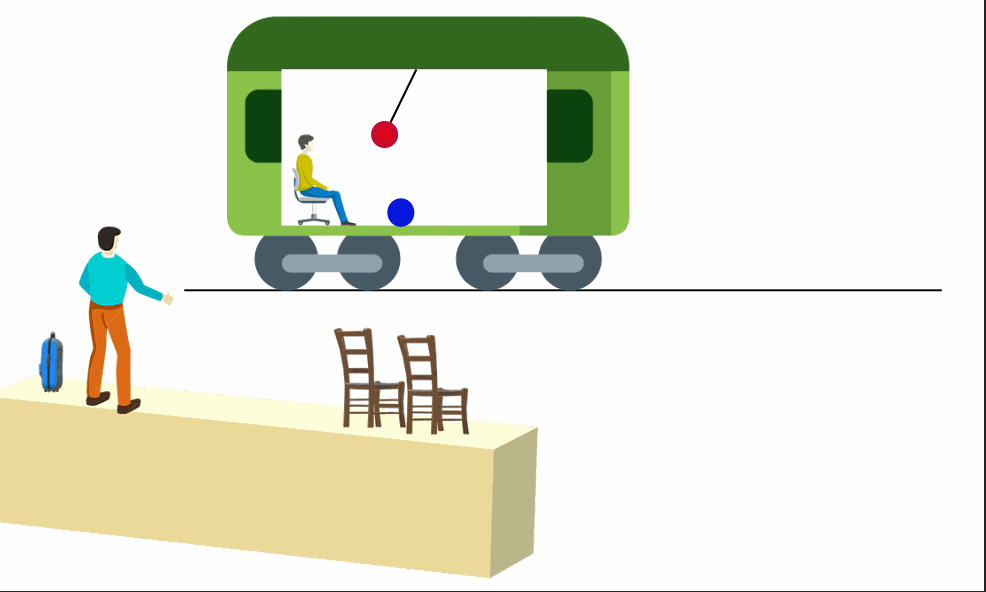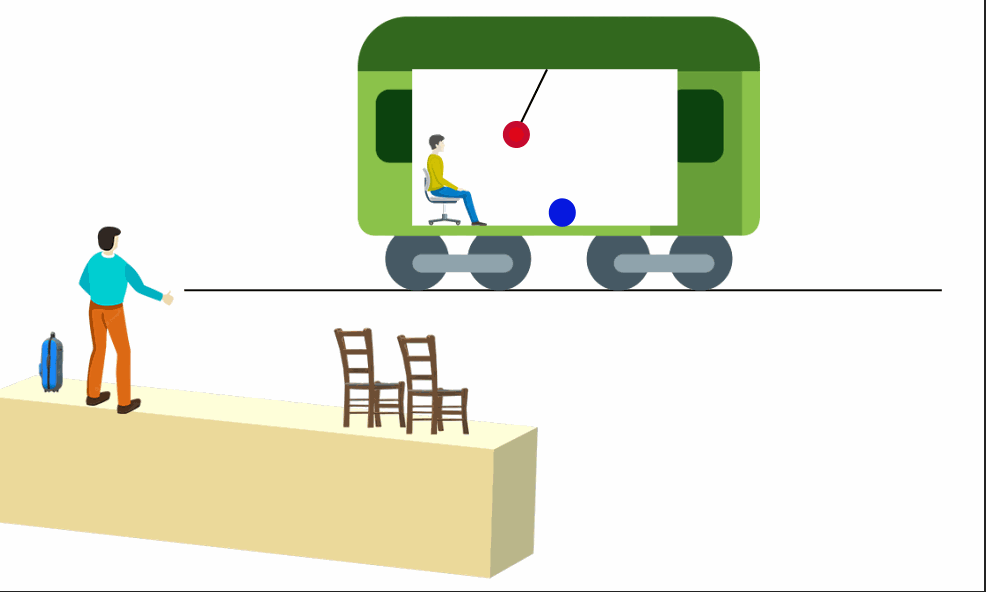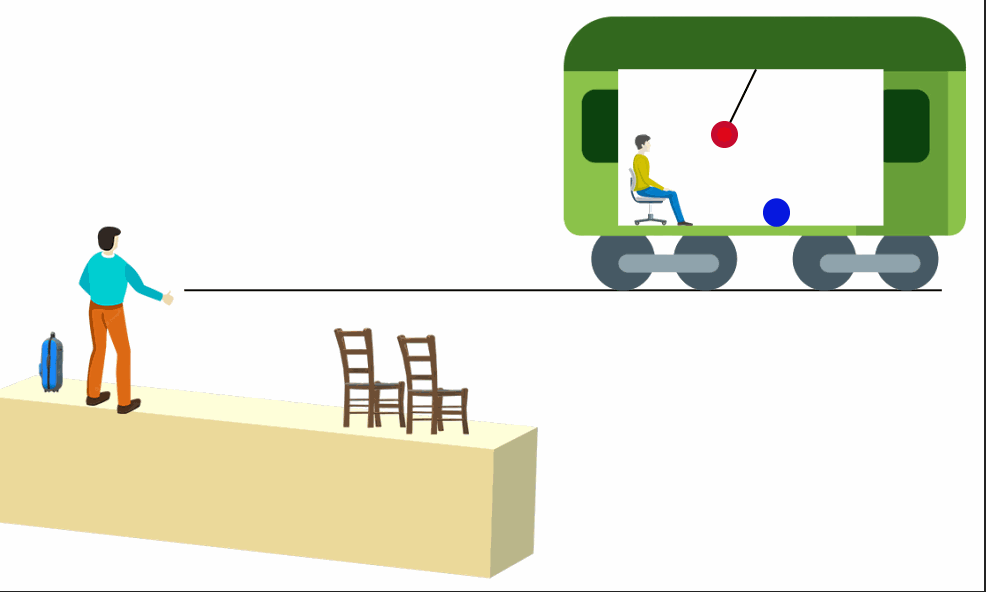
Um vagão sobre trilhos está em movimento retilíneo e uniforme em relação a um observador fixo na plataforma. Ele desliza suavemente de modo que observadores dentro do vagão não sintam nenhuma trepidação. Além disso, ele está totalmente fechado. A pessoa dentro do vagão não pode ver o exterior, mas o observador na plataforma pode ver o acontece em seu interior.
Considere também que um pêndulo está preso ao teto do trem e uma bolinha de gude move-se sobre o piso do vagão em MRU.
Quais seriam as percepções de um observador dentro do trem e de outro referencial fixo na Terra? Seriam equivalentes? Esses observadores concordariam um com o outro quando se encontrarem para conversar?
Como a pessoa que está dentro do trem não percebe seu próprio movimento, tudo se passa, como se o vagão estive parado.
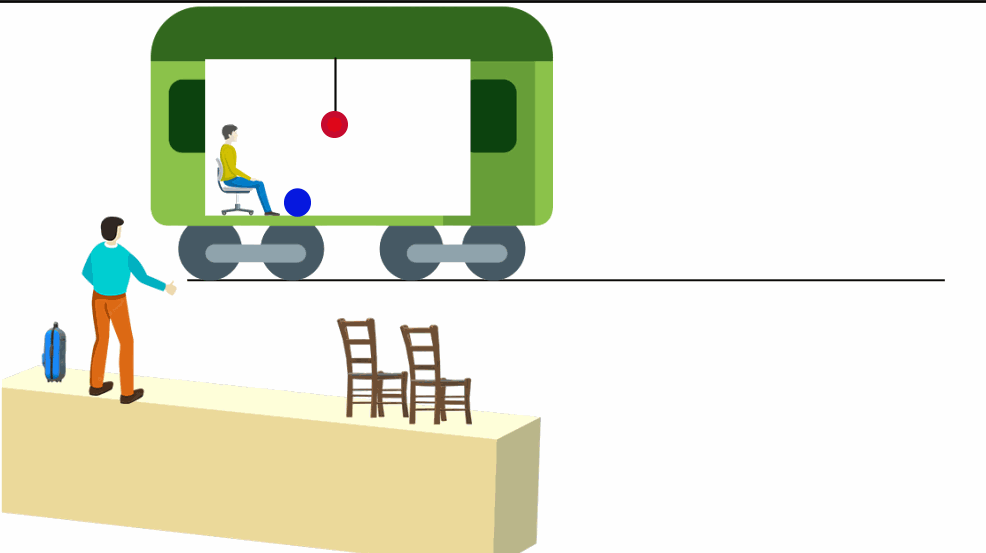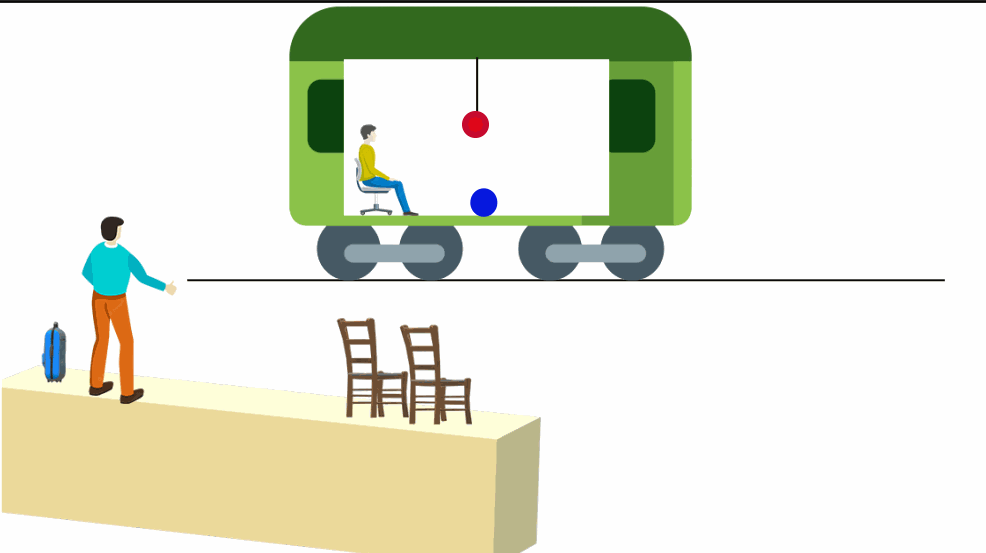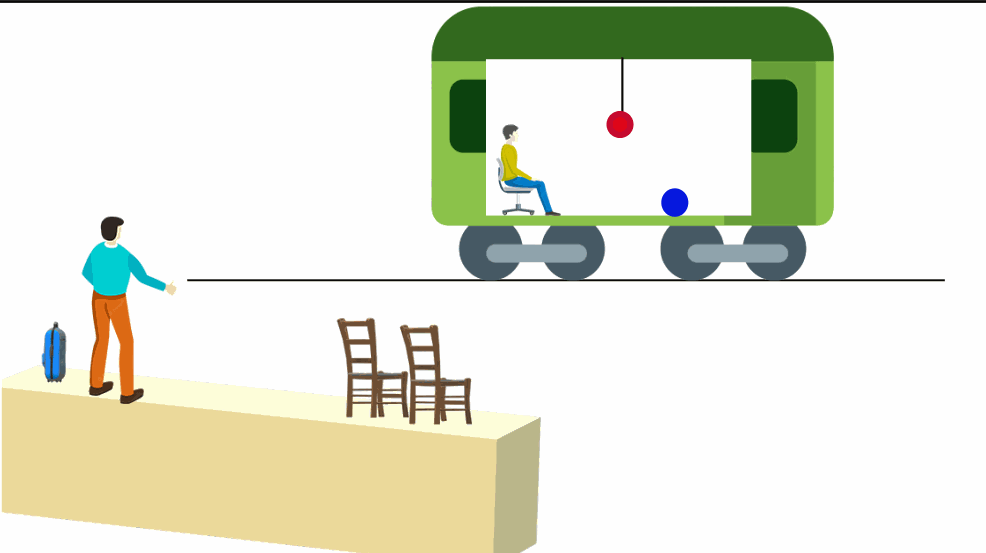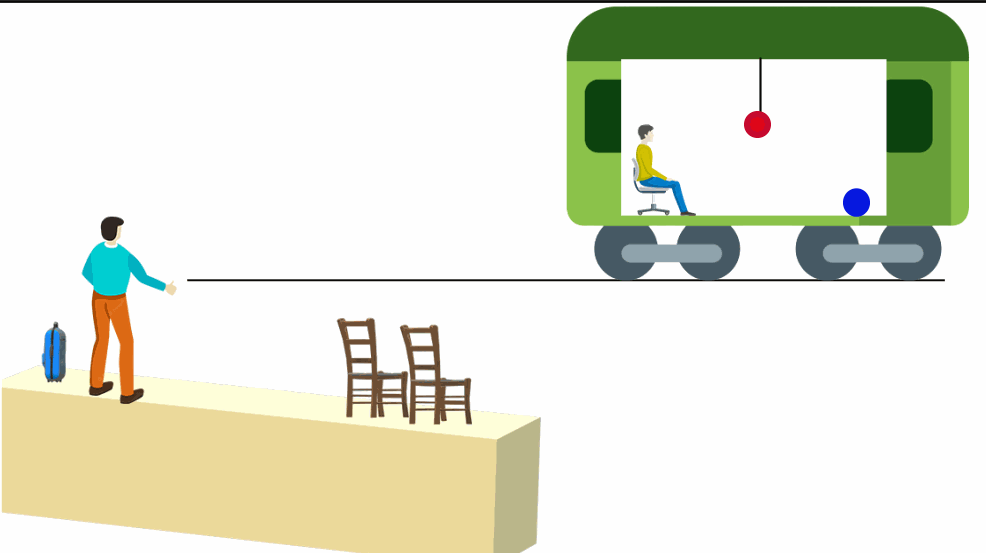

O pêndulo permaneceria pendurado verticalmente ao teto e a bolinha descreveria seu movimento normalmente.
Assim como o referencial do trem, o observador da estação descreveria tudo dentro do vagão de forma a obedecer as leis de Newton. O pêndulo estaria vertical e a bolina moveria dentro do vagão.
A única diferença entre eles seria a seguinte. Para o referencial dentro do vagão tudo estaria em repouso com velocidade zero, exceto a bolinha sobre o piso. Para o observador da estação tudo dentro do vagão estaria com certa velocidade horizontal. Porém, a velocidade da bolinha seria igual à velocidade do trem em relação à estação somada à velocidade da bolinha em relação ao vagão.
Então, podemos dizer que ambos os observadores concordam que as Leis de Newton estão em pleno "funcionamento" para ambos referenciais, e por isso, os dois são referenciais inerciais.
Mas, e se... O vagão estiver acelerado para frente em relação à estação? Epa, aí as coisas mudam de figura.
Ambos observadores concordariam que o pêndulo estaria deslocado para trás, e a velocidade da bolinha não seria mais constante. Então, para a pessoa dentro do trem as Leis de Newton pareceriam estranhas. O vagão, portanto, não é um referencial inercial. Ele, sentado e em repouso sentiria uma "pressão para trás" e questionaria: como o pêndulo pode estar em repouso, mas inclinado? E a bolinha que não descreve o MRU?

O próprio Newton apresentou uma boa resposta para esses questionamentos identificando os limites de suas leis. Ele chamou de referenciais inerciais aqueles que estão em repouso ou movimento retilineo uniforme em relação ao espaço absoluto ou em relação um ao outro. Nesses referenciais, as leis de Newton são perfeitamente válidas, apesar de não ser possível saber se o referencial está em repouso ou MRU. Mas, isso não tem problema, pois ambos os estados são equivalentes.
Se um referencial possui alguma aceleração em relação ao espaço absoluto, entendido como uma estrutura infinita e homogênea na qual os corpos estão localizados, as leis de Newton não se aplicam e o referencial não é inercial.
Em resumo, não existe experimento capaz de identificar se um referencial está em repouso ou MRU. No entanto, é possível descobrir se um referencial está acelerado.
Interessante notar que com essa formulação de Newton é possível saber se a Terra gira em torno do seu próprio eixo, sendo, portanto, um referencial não inercial. Ele desenvolveu cálculos precisos que puderam ser confirmados com as famosas experiências dos pêndulos de Foucault.
Então, tudo certo até o momento. Só que a ciência anda. Outros ramos da Física entrarão em cena.
Sequência de posts em direção à teoria de Relatividade de Einstein
